Un framework per la simulazione di modelli ad agenti mobili

Alessio Cantarella
a cura di Mattia Frasca (relatore), Stefano Fazzino (correlatore)
ℹ️ Facoltà di Ingegneria / Università degli Studi di Catania, a.a. 2010/2011

Indice

1. Introduzione
2. Modelli ad agenti mobili
3. Strumenti utilizzati
4. Implementazione sequenziale
5. Implementazione parallela
6. Valutazioni
7. Conclusioni

1. Introduzione

Questa tesi di laurea verte sulla descrizione di un framework per la simulazione di modelli ad agenti mobili, progettato e realizzato presso il Dipartimento di Ingegneria Elettrica, Elettronica e Informatica (DIEEI) dell’Università degli Studi di Catania.
Nei primi capitoli, forniremo una breve presentazione teorica degli argomenti trattati e degli strumenti utilizzati.
Successivamente, passeremo alla descrizione vera e propria del software, di cui sono state implementate due differenti versioni (una sequenziale e una parallela).
Infine, attraverso i dati statistici ottenuti dalle simulazioni, valuteremo i risultati e le prestazioni, per trarre delle conclusioni sugli eventuali vantaggi della parallelizzazione del codice.

2. Modelli ad agenti mobili

Consideriamo un sistema di n agenti identici (“random walker”), che vagano indipendentemente all’interno di un piano quadrato di lato l.
Fissare l equivale a definire la densità degli individui

ρ = n / l².

Gli agenti sono rappresentati da particelle puntiformi, le cui posizioni e velocità al tempo t sono indicate, rispettivamente, come

y_i (t) = [y_{i, 1} (t), y_{i, 2} (t)],
v_i (t) = [y_i (t) cos θ_i (t), v_i (t) sin θ_i (t)], (2.1)

∀ i ∈ {1, …, n}.
Supponiamo che l’area, in cui gli agenti si muovono, sia caratterizzata da condizioni di periodicità ai bordi, ovvero

y_{i, j} = y_{i, j} + l se y_{i, j} < l / 2,
y_{i, j} = y_{i, j} – l se y_{i, j} ≥ l / 2,

∀ i ∈ {1, …, n} e ∀ j ∈ {1, 2}.
Inoltre, ipotizziamo che gli agenti si muovano con una velocità il cui modulo è costante nel tempo e uguale per tutti, cioè

v_i (t) = v,

da cui la (2.1) diventa

v_i (t) = [v cos θ_i (t), v sin θ_i (t)],

∀ i ∈ {1, …, n} e ∀ t.
All’istante t = 0, le particelle sono distribuite casualmente; mentre, per ogni t successivo, cambiano stocasticamente gli angoli delle loro direzioni θ_i (t), ∀ i ∈ {1, …, n}, in accordo con l’equazione

θ_i (t) = ξ_i (t),

dove ξ_i (t) sono n variabili aleatorie indipendenti, distribuite identicamente e scelte con probabilità uniforme nell’intervallo [-π, π].
Le posizioni delle particelle, invece, sono aggiornate secondo la regola

y_i (t + 1) = y_i (t) + v_i (t). (2.2)

Per includere l’ipotesi che gli agenti possano muoversi nel nostro mondo bidimensionale con scale temporali più brevi, come nel caso di individui che viaggiano in aereo, definiamo il parametro p_J ∈ [0, 1], che quantifica la probabilità che un agente “salti” in una posizione completamente casuale all’interno del piano: per ogni istante, ciascun agente evolve secondo l’equazione (2.2) con probabilità 1 – p_J oppure effettua un salto con probabilità p_J.
Infine, fissiamo un raggio di interazione r = 1, che definisce la rete di interazione istantanea: per ogni istante, ogni individuo interagisce solo con gli agenti che si trovano all’interno del suo vicinato di raggio r.

2.1 Diffusione delle epidemie

Molti sistemi sociali e di telecomunicazioni possono essere modellati con delle reti complesse.
Capire i meccanismi mediante i quali le informazioni, i disturbi, i virus o, come nel caso in questione, le malattie vi si diffondono è una delle ragioni principali per cui tali reti sono studiate.
In particolare, nello studio teorico della diffusione delle epidemie, è importante considerare che sia la natura dello stato finale, sia la dinamica del processo sono fortemente influenzate dalla topologia delle connessioni della rete sottostante: ad esempio, nei sistemi small-world, che sono caratterizzati da percorsi brevi (i cosiddetti “sei gradi di separazione”), la diffusione è più veloce.
Inoltre, la soglia epidemica è influenzata dalle proprietà della distribuzione di grado Γ (k): ad esempio, nelle reti scale-free, la divergenza del momento di secondo ordine di Γ (k) porta al sorprendente risultato dell’assenza di una soglia epidemica e, di conseguenza, del suo comportamento critico.

2.1.1 Stato dell’arte

Ad oggi, la maggior parte dei risultati presenti in letteratura si riferisce a modelli in cui la diffusione della malattia avviene su una topologia statica, cioè dove la rete sottostante non varia nel tempo.
In tal caso, gli agenti sono situati in posizioni fisse, connesse da un grafo, e l’evoluzione dello stato di un individuo dipende solo dagli stati dei suoi vicini nel grafo.
Tuttavia, una possibilità più realistica è considerare le reti stesse come delle entità dinamiche, dove la topologia è tempo-variante.
Il problema in questione è stato affrontato anche su reti adattive, nelle quali gli agenti suscettibili hanno la percezione del rischio dell’infezione e, modificando le loro connessioni, sono in grado di evitare i contatti con quelli infetti: in tal caso, la rete è pilotata dall’interno, dal processo di diffusione.
Nel nostro modello, invece, ci concentriamo sul caso in cui la rete (dinamica) è pilotata dall’esterno, dal moto spaziale degli agenti.

2.1.2 Il nostro modello

Fra tutti i possibili meccanismi di diffusione delle malattie – SIS, SIRI, SIRS, SI, ecc. –, focalizziamo la nostra attenzione sul modello SIR (Susceptible, Infective and Recovered), che classifica gli agenti in tre stati distinti: suscettibili (S), infetti (I) e guariti (R).
Indichiamo con n_S (t), n_I (t) e n_R (t), rispettivamente, i numeri di agenti nei tre gruppi appena elencati al tempo t e con la costante

n = n_S (t) + n_I (t) + n_R (t)

il numero totale di agenti.
All’istante t = 0, una piccola percentuale di agenti q_I è infetta e rappresenta il seme della malattia, mentre tutti gli altri sono suscettibili.
Per i passi successivi, la probabilità che un agente venga infettato cresce all’aumentare del numero di individui nel suo vicinato.
Più precisamente, un agente nello stato S, che abbia esattamente un infetto tra i suoi vicini, passerebbe allo stato I con probabilità p_I o resterebbe nello stato S con probabilità 1 − p_I; se, invece, il numero di individui infetti nel vicinato di un agente suscettibile fosse m_I, allora la sua probabilità di diventare infetto sarebbe 1 − (1 − p_I)^m_I.
Infine, ogni agente infetto può passare con probabilità p_R allo stato R, dove non può più contrarre la malattia.
Di conseguenza, la durata media di un’infezione è 1 / p_R.

2.2 Evoluzione della cooperazione

Capire come la cooperazione possa emergere in una popolazione di individui egoisti è un problema aperto nel campo della biologia e delle scienze sociali.
Un aiuto fondamentale nella comprensione di questo fenomeno proviene dalla teoria dei giochi: sviluppando e studiando vari dilemmi sociali, gli studiosi hanno fatto luce molti meccanismi che favoriscono un comportamento cooperativo nelle popolazioni.
In particolare, uno dei più approfonditi è il dilemma del prigioniero, un gioco a due giocatori, ognuno dei quali può scegliere di adottare una delle due strategie disponibili: cooperare o disertare.
Sebbene una popolazione di individui ben combinati porti generalmente alla diserzione, l’esistenza di una struttura spaziale fa sì che la cooperazione possa sopravvivere sotto certe condizioni (ad esempio, la costituzione di cluster cooperativi).

2.2.1 Stato dell’arte

Di recente, è stato dimostrato che il comportamento cooperativo aumenta quando gli individui giocano all’interno di reti complesse: e.g., nelle reti scale-free la cooperazione si sviluppa nei nodi fortemente connessi, i quali rendono cooperatori gli agenti del loro vicinato.
Inoltre, per garantire miglioramenti al grado di cooperazione nel sistema, sono stati studiati vari meccanismi, basati su tecniche di riconnessione, crescita e adattamento.
I modelli evolutivi ad agenti mobili, invece, non sono ancora stati approfonditi del tutto e li analizziamo nel nostro modello.

2.2.2 Il nostro modello

Per studiare le dinamiche evolutive, supponiamo che i nostri individui mobili interagiscano tra loro, giocando al dilemma del prigioniero. Inizialmente, i giocatori adottano una delle due strategie disponibili: cooperare (C) o disertare (D), con la stessa probabilità

p_C = p_D = 1 / 2.

I risultati di una partita si traducono nei guadagni seguenti: se tutt’e due gli agenti attuassero la stessa strategia, riceverebbero g_CC per una mutua cooperazione o g_DD per una mutua diserzione; altrimenti, se adottassero strategie differenti, g_CD andrebbe al cooperatore e g_DC al disertore. Nel gioco in questione, questi valori sono ordinati come

g_DC > g_CC > g_DD ≥ g_CD,

quindi la diserzione è la scelta migliore, indipendentemente dalla scelta dell’avversario.
Ogni agente, dopo aver giocato con tutti i suoi vicini (il vicinato di ogni individuo cambierà continuamente), accumula i guadagni ottenuti in ogni partita e, confrontando questi ultimi con quelli del suo primo vicino, decide se continuare a utilizzare la stessa strategia o no.
Durante questo processo (che avviene in maniera sincrona per tutti gli individui del sistema), l’agente i sceglie casualmente uno dei suoi vicini, j, e confronta i rispettivi guadagni, g_i e g_j: se g_i ≥ g_j, non accade nulla e i continua a giocare con la stessa strategia; al contrario, se g_i < g_j, l’agente i adotta la strategia di j con una probabilità proporzionale alla differenza dei guadagni

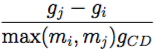
dove m_i e m_j sono i vicini istantanei di i e j. Una volta fatto ciò, azzeriamo i guadagni, in modo da non considerare la versione iterata del gioco.

2.3 Sincronizzazione del caos

Il problema della sincronizzazione del caos (ad esempio, il regime in cui due o più oscillatori caotici evolvono, seguendo la stessa traiettoria caotica, indipendentemente dalle loro differenti condizioni iniziali), è un comportamento dinamico molto interessante, studiato sotto molti punti di vista.
Un caso di particolare interesse è quando gli oscillatori sono i nodi di una rete complessa e le connessioni rappresentano i loro accoppiamenti.

2.3.1 Condizioni per la sincronizzazione

Linearizzando le dinamiche della rete intorno alla varietà di sincronizzazione, si possono ricavare le condizioni affinché n oscillatori identici (accoppiati da un’arbitraria configurazione di rete che ammetta una varietà di sincronizzazione) si sincronizzino.
Si consideri che la dinamica di ogni nodo è descritta da

ẋ_i = F (x_i) – k g_{i, j} H (x_j),

∀ i ∈ {1, …, n}, dove x_i è un vettore N-dimensionale delle variabili dinamiche del nodo i, ẋ_i = F (x_i) rappresenta la dinamica di ogni nodo isolato, k è il coefficiente di accoppiamento, H : ℝ^N → ℝ^N è la funzione di accoppiamento e G = (g_{i, j}) è la matrice n × n (con soglia a somma-zero) che modella le connessioni di rete (i.e., il laplaciano della rete).
La dinamica del sistema linearizzato è rappresentata dall’equazione variazionale diagonalizzata a blocchi

ξ˙ = (J_F – k γ_h J_H) ξ_h, (2.3)

∀ h ∈ {1, …, N}, dove γ_h è l’autovalore h-esimo di G, J_F e J_H sono, rispettivamente, le matrici jacobiane di F e H, calcolate attorno allo stato sincrono e uguali per ogni blocco; dunque, i blocchi della (2.3) differiscono l’un l’altro solo per il termine k γ_h.
Se volessimo studiare le proprietà di sincronizzazione per differenti topologie, dovremmo considerare la (2.3) in funzione di un generico autovalore (complesso) α + i β, definire la Master Stability Equation (MSE)

ζ˙ = [J_F – (α + i β) J_H] ζ (2.4)

e analizzare il massimo esponente di Lyapunov λ_max della (2.4) in funzione di α e β, ottenendo la Master Stability Function (MSF)

λ_max = λ_max (α + i β). (2.5)

Quindi, la stabilità della varietà di sincronizzazione in una certa rete può essere valutata calcolando gli autovalori γ_h della matrice G e studiando il segno di λ_max nei punti

α + i β = k γ_h,

∀ h ∈ {2, …, n}: se tutti i nodi sono stabili ∀ h ∈ {2, …, n}, allora anche lo stato sincrono è stabile per il dato valore di k; se G ha autovalori reali, allora la 2.5 può essere calcolata solo in funzione di α.
Il formalismo della MSF ci permette di studiare come la topologia influenzi la tendenza alla sincronizzazione di una rete: in particolare, fornisce una condizione necessaria – la negatività di tutti gli esponenti di Lyapunov – per la stabilità di un processo di sincronizzazione completa.

2.3.2 Il nostro modello

Nel nostro modello, supponiamo che a ogni agente sia associato un oscillatore caotico, accoppiato esclusivamente con quelli dei vicini.
Questa situazione può essere considerata una buona rappresentazione di vari problemi, come la coordinazione di sciami di animali (i quali non solo sono in grado di coordinare i loro movimenti nel piano, ma anche di reagire contemporaneamente se soggetti a pericoli o attacchi), la sincronizzazione dei clock dei robot mobili (in cui la comunicazione è limitata dal range del sistema di comunicazione) o la comparsa di oscillazioni sincronizzate in una sospensione di cellule di lievito (osservata empiricamente per densità sufficientemente elevate).
Quindi, un sistema caotico dinamico è associato a ogni agente, caratterizzato da un vettore di variabili di stato x_i (t) ∈ ℝ^N, che evolve secondo una legge caotica.
Senza perdita di generalità, mettiamoci sotto l’ipotesi di fast switching e consideriamo il caso degli oscillatori di Rössler, dove la dinamica di stato di ogni agente è descritta da

ẋ_{i, 1} = –(x_{i, 2} + x_{i, 3}),
ẋ_{i, 2} = x_{i, 1} + a x_{i, 2},
ẋ_{i, 3} = b + x_{i, 3} (x_{i, 1} – c),

con

x_i (t) = ,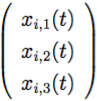

a = 0.2, b = 0.2 e c = 7.
Quando due agenti interagiscono, le equazioni di stato di ogni individuo cambiano per includere l’accoppiamento diffusivo con il vicino, agendo sulla variabile di stato x₁.
Basandoci su queste ipotesi, la dinamica di stato di ogni agente può essere descritta dalle seguenti equazioni:

ẋ_i (t) = F (x_i (t)) – k g_{i, j} (t) E x_j (t), (2.6)

∀ i ∈ {1, …, n}, dove F : ℝ³ → ℝ³ è data dalla dinamica di Rössler, e nel caso esaminato si è fissato

E =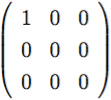

e g_{i, j} (t) sono gli elementi di una matrice tempo-variante G (t), che definisce il vicinato di ogni agente al tempo t e dipende dalla traiettoria di ogni agente; più in dettaglio, all’istante t: g_{i, j} (t) = g_{j, i} (t) = –1 se gli individui i e j sono vicini; g_{i, j} (t) = g_{j, i} (t) = 0 se gli individui i e j non sono vicini; infine, g_{i, i} = m, dove m è il numero di vicini dell’agente i.
Di conseguenza, le equazioni (2.6) possono essere riscritte come:

ẋ_{i, 1} = –(x_{i, 2} + x_{i, 3}) – k g,
ẋ_{i, 2} = x_{i, 1} + a x_{i, 2},
ẋ_{i, 3} = b + x_{i, 3} (x_{i, 1} – c),

con

g = (x_{j, 1} – x_{i, 1}).

Nel seguito si assumerà sempre un passo di integrazione ∆ t = 0.001.
Per l’analisi dei risultati della simulazione (di durata T = 500), definiamo l’errore di sincronizzazione

e (t) =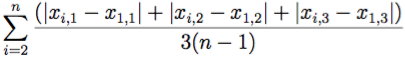

e l’indice di sincronizzazione

δ (t) =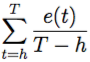

che rappresenta semplicemente la media di e, calcolata nell’intervallo [h, T], con h = 0.8 T.

3. Strumenti utilizzati

In questo capitolo, descriviamo i software utilizzati per realizzare il framework: il linguaggio di programmazione Python, la tecnologia OpenCL, alcune librerie per Python (Matplotlib, NumPy e PyOpenCL) ed il generatore di numeri casuali MWC64X.

3.1 Python

Python è un linguaggio di programmazione interpretato, interattivo e orientato agli oggetti, che Guido Van Rossum ideò per tenersi occupato durante le vacanze natalizie del 1989.
Python fa della dinamicità, semplicità e flessibilità i suoi principali obiettivi, ed è un linguaggio multi-paradigma: supporta sia la programmazione orientata agli oggetti, sia quella strutturata.

3.1.1 Caratteristiche

Le caratteristiche più immediatamente riconoscibili di Python sono le variabili non tipizzate (il controllo dei tipi è comunque forte e viene eseguito a runtime), l’uso dell’indentazione per la definizione dei blocchi e la presenza di un ricco assortimento di tipi e funzioni di base, e librerie standard (che favoriscono lo sviluppo di applicazioni molto complesse). Generalmente, Python è considerato un linguaggio interpretato: in realtà, il codice sorgente non viene direttamente convertito in linguaggio macchina, ma passa prima da una fase di pre-compilazione in bytecode; lo stesso bytecode viene quasi sempre riutilizzato dopo la prima esecuzione del programma, evitando così di dover ogni volta interpretare il sorgente e incrementando di conseguenza le prestazioni.

3.1.2 Prestazioni

Se paragonato ai linguaggi compilati tipizzati staticamente (e.g., il C), la velocità di esecuzione non è uno dei punti di forza di Python, specialmente nel calcolo matematico; le prestazioni sono invece allineate o addirittura superiori ad altri linguaggi interpretati (quali, ad esempio, il PHP e il Ruby).

3.2 OpenCL

Negli ultimi anni, le unità di elaborazione grafica (GPU) si sono evolute da semplici chip single-purpose a processori flessibili, che garantiscono prestazioni un tempo riservate solo a ingombranti supercomputer. OpenCL (Open Computing Language) è un framework – composto da un linguaggio, un’API e un runtime –, che permette a qualsiasi applicazione di attingere alla vasta potenza di calcolo delle schede grafiche, avendo così incredibili opportunità prestazionali.

3.2.1 Prestazioni e parallelismo

Ogni nuova generazione di GPU aumenta le capacità di rendering (cioè la tecnica che utilizza colori e ombre su un’immagine piana per farla apparire solida e tridimensionale), migliorando la fedeltà, il realismo e la risoluzione: le schede grafiche di oggi sono capaci di traslare miliardi di pixel al secondo (ogni pixel è il risultato finale di un insieme complesso di operazioni matematiche).
Dal punto di vista computazionale, le GPU eseguono operazioni con livelli prestazionali pari a quelli dei supercomputer; le più veloci, addirittura, eseguono circa un bilione di calcoli al secondo (1000 GFLOPS). Dietro il notevole aumento della potenza di calcolo c’è un incremento impressionante della quantità di lavoro eseguito in parallelo: poiché sugli schermi dei computer ci sono milioni di pixel, il modo per elaborarli più velocemente è operare su più di uno per volta.
Oggigiorno, i progettisti includono nelle loro schede una grande quantità di elementi in grado di operare sui pixel: più ce ne sono, più la GPU può effettuare velocemente i suoi calcoli e produrre i risultati sullo schermo.

3.2.2 Al di là della grafica

Le prime schede video furono progettate per implementare gli standard della programmazione grafica, come OpenGL.
Il forte accoppiamento tra il linguaggio utilizzato dai programmatori grafici e i contenuti dei chip assicurava buone prestazioni per la maggior parte delle applicazioni, ma limitava le capacità della scheda solo a ciò che era definito nel linguaggio grafico.
Per superare questo limite, i progettisti resero gli elementi per le operazioni sui pixel personalizzabili utilizzando dei programmi specifici, detti shader grafici.
Col passare del tempo, gli shader si evolsero da semplici programmi in linguaggio assembly a programmi di alto livello, con i quali è possibile creare gli scenari sorprendenti che si trovano sui software 3D di oggi.
Dunque, per gestire la crescente complessità degli shader, gli elementi di elaborazione dei pixel e dei vertici furono riprogettati per supportare le più generiche operazioni matematiche, logiche e di controllo del flusso. A questo punto, Apple provò a portare le GPU oltre il semplice utilizzo grafico: tutto quello che serviva era un’API non-grafica, che potesse coinvolgere i suddetti aspetti di programmazione delle schede video.
La tecnologia che fornisce alle applicazioni i mezzi per accedere alle eccezionali prestazioni delle moderne GPU è OpenCL.

3.2.3 Framework

OpenCL è un framework completamente progettato per accelerare le prestazioni delle applicazioni – utilizzando le GPU per calcoli general-purpose – ed è composto da un linguaggio basato sul C (con supporto al parallelismo) e un’API, che permette alle applicazioni di utilizzare uno o più dispositivi compatibili (GPU, CPU, ecc.) nel proprio sistema.
Il nome è stato pensato in analogia a OpenGL e OpenAL, in quanto tutti standard industriali aperti, pur con diverse finalità: il primo per sfruttare le potenzialità delle attuali GPU oltre il rendering grafico, e gli altri rispettivamente per la grafica 3D e il rendering audio posizionale.

3.2.4 Linguaggio

OpenCL-C è una variante del più familiare linguaggio C99, ottimizzato per la programmazione parallela nelle GPU.
È stato incluso un supporto completo ai tipi vettoriali per garantire un migliore flusso dei dati e aumentare l’efficienza, inoltre, sono stati definiti dei requisiti di precisione numerica (basati sullo standard IEEE 754-2008) con lo scopo di fornire dati consistenti utilizzando hardware di differenti produttori.
Quindi, OpenCL è utilizzato per riscrivere solo i frammenti di codice che richiedono prestazioni elevate o che fanno un uso intenso di dati.
Durante il processo di riscrittura, l’applicazione è scomposta fino al suo stato più elementare: una serie di operazioni discrete, le quali descrivono i calcoli che possono essere eseguiti in parallelo su un insieme di dati.
Il codice risultante (.cl) è detto kernel ed è simile a una funzione C tradizionale, ma, a differenza di quest’ultima, i kernel OpenCL sono incorporati nell’applicazione in uno stato non compilato: solo poco prima di essere inviati alla GPU, essi verranno compilati “al volo” e ottimizzati per l’hardware specifico.

3.2.5 API

Un’API (Application Programming Interface) è un sistema di strumenti e risorse, che permette agli sviluppatori di creare applicazioni software. OpenCL-API fornisce delle funzioni che permettono di gestire task di calcolo parallelo: elenca l’hardware nel sistema compatibile con OpenCL, imposta la condivisione di strutture dati tra l’applicazione e OpenCL, controlla il processo di compilazione e presentazione dei kernel alla GPU, gestisce l’accodamento e la sincronizzazione, ecc.

3.2.6 Runtime

OpenCL-runtime esegue i task presentati dall’applicazione tramite l’API: trasferisce efficientemente i dati tra la memoria principale e la VRAM dedicata usata dalla GPU, e controlla l’esecuzione dei kernel sull’hardware della scheda video.
Inoltre, durante l’esecuzione, il runtime gestisce le dipendenze in-order o out-of-order tra i kernel, e utilizza gli elementi di elaborazione della GPU nella maniera più efficiente.

3.2.7 Flusso di lavoro

All’inizio, l’applicazione chiama l’API per determinare quali dispositivi sono disponibili all’interno del sistema e, dopo aver selezionato quello appropriato, crea una coda di comandi, carica e compila i kernel C che utilizzerà e, quando è pronta per eseguire un kernel, chiama l’API per specificare i dati e il numero di istanze kernel parallele necessarie.
Il runtime copia sulla VRAM della GPU i dati richiesti dal kernel e la GPU esegue simultaneamente i kernel sui suoi elementi di elaborazione. Questa esecuzione parallela dei kernel causa delle prestazioni nettamente superiori rispetto alle tecniche di programmazione tradizionali, come il multithreading (ad esempio, utilizzando una GPU con 200 elementi di elaborazione, OpenCL esegue 1000 calcoli in sole 5 iterazioni!). Durante l’esecuzione, OpenCL gestisce le dipendenze in-order e out-of-order tra i kernel, in modo da schedulare anche task molto complessi, composti da più kernel, per eseguirli efficientemente su tutti gli elementi di elaborazione della GPU.
Inoltre, tutti i calcoli sono effettuati in modalità asincrona: mentre la GPU esegue i suoi kernel, l’applicazione può continuare ad eseguire il suo thread principale sulla CPU.

3.2.8 Standard

Nel 2008, Apple, AMD, Intel e NVIDIA proposero al consorzio Khronos Group le basi per lo standard e, nel dicembre dello stesso anno, OpenCL fu ufficialmente approvato come uno standard “aperto e royalty-free”.
Allo stato attuale, OpenCL è supportato su chipset AMD, NVIDIA e Intel, è certificato sul sistema operativo Mac OS X Snow Leopard ed è disponibile in versione beta su Windows e Linux.

3.3 Matplotlib

Matplotlib è una libreria per Python, scritta da John Hunter, che ci servirà a produrre grafici in 2D.

3.4 NumPy

NumPy è una libreria per Python, contenente strumenti per il calcolo scientifico, che utilizzeremo per gestire vettori a n dimensioni.

3.5 PyOpenCL

PyOpenCL è una libreria per Python, realizzata da Andreas Klöckner, che permette di accedere all’API di OpenCL (e, di conseguenza, ai benefici della programmazione parallela), direttamente da un programma scritto in Python (.py), detto host.
Vediamo, tramite un semplice esempio, com’è possibile parallelizzare (nell’host parallel_example.py e nel kernel parallel_example.cl) un’applicazione sequenziale sequential_example.py, che, dati tre vettori a, b e c (tutt’e tre di dimensione n), moltiplica a_i e b_i per m volte, e mette il risultato in c_i, ∀ i ∈ {1, …, n}.

3.5.1 Esempio sequenziale

Importiamo le librerie necessarie: numpy e time (per calcolare il tempo di esecuzione).
Definiamo le variabili di ingresso: la dimensione dei vettori n e il numero di iterazioni m.
Definiamo le variabili di uscita: i vettori a, b e c.
Definiamo la funzione sf, che simula – in maniera sequenziale – il nostro codice di esempio.
La funzione __main__ chiama sf e stampa il tempo impiegato dalla simulazione.

# sequential_example.py

import numpy, time

n = 1000
m = 5000

a = numpy.random.rand(n).astype(numpy.float32)
b = numpy.random.rand(n).astype(numpy.float32)
c = numpy.empty_like(a).

def sf():
  for i in range(n):
    for j in range(m):
      c[i] = a[i] * b[i]

if __name__ == "__main__":
  t1 = time.time()
  sf()
  t2 = time.time()
  print "Elapsed time: ", t2 - t1, " s"

3.5.2 Esempio parallelo

Importiamo le librerie necessarie: numpy, pyopencl e time (per calcolare il tempo di esecuzione).
Definiamo le variabili di ingresso: la dimensione globale dei vettori n, il numero di iterazioni m e il nome del file OpenCL f.
Definiamo le variabili di uscita: i vettori a, b e c.
Definiamo la funzione host pf, che simula – in modo parallelo – il nostro codice di esempio. Definiamo le variabili OpenCL: la coda dei comandi cq e il programma p. Definiamo i buffer OpenCL: ai e bi in ingresso (cioè, a cui passiamo i dati da copiare sulla GPU), e co in uscita (ovvero, che utilizziamo per conservare i risultati delle operazioni). Invochiamo la funzione kernel pf, a cui passiamo: la coda dei comandi, la dimensione globale e locale dei vettori, il numero di iterazioni, e i buffer. Copiamo il contenuto del buffer co in c.
La funzione __main__ chiama pf, a cui passa cx (se nella piattaforma vi fossero più dispositivi compatibili con OpenCL, all’utente verrebbe chiesto di sceglierne uno), e stampa il tempo impiegato dalla simulazione.

# parallel_example.py (host)

import numpy, pyopencl, time

n = 1000
m = 5000
f = "parallel_example.cl"

a = numpy.random.rand(n).astype(numpy.float32)
b = numpy.random.rand(n).astype(numpy.float32)
c = numpy.empty_like(a).

def pf(cx):
  cq = pyopencl.CommandQueue(cx)
  p = pyopencl.Program(cx, "".join(open(f, 'r').readlines())).build(options = "−I ./")
  ai = pyopencl.Buffer(cx, pyopencl.mem_flags.READ_ONLY | pyopencl.mem_flags.COPY_HOST_PTR, hostbuf = a)
  bi = pyopencl.Buffer(cx, pyopencl.mem_flags.READ_ONLY | pyopencl.mem_flags.COPY_HOST_PTR, hostbuf = b)
  co = pyopencl.Buffer(cx, pyopencl.mem_flags.WRITE_ONLY, b.nbytes)
  p.pf(cq, a.shape, None, m, ai, bi, co)
  pyopencl.enqueue_read_buffer(cq, co, c).wait().

if __name__ == "__main__":
  cx = pyopencl.create_some_context()
  t1 = time.time()
  pf(cx)
  t2 = time.time()
  print "Elapsed time: ", t2 − t1, " s"

La funzione kernel pf riceve dall’host: il numero di iterazioni m, in ingresso ai e bi, e in uscita co.
Definiamo l’unica variabile utile: l’identificativo (ID) globale i dell’elemento. Aggiorniamo il valore di co dell’elemento i-esimo.

# parallel_example.cl (kernel)

__kernel void pf(
  uint m,
  __global const float ∗ai,
  __global const float ∗bi,
  __global float ∗co
) {
  int i = get_global_id(0);
  for (int j = 0; j < m; j++)
    co[i] = ai[i] * bi[i];
}

3.5.3 Valutazioni

I tempi medi di esecuzione (calcolati su 10 differenti realizzazioni) del codice sequenziale e parallelo sono, rispettivamente, 4.14 s e 0.017 s.
In parole povere, l’implementazione parallela è circa 250 volte più veloce di quella sequenziale!

3.6 MWC64X

Poiché in OpenCL non sono integrate funzioni per la generazione di numeri casuali, è necessario crearne una.
MWC64X è un generatore di numeri casuali (RNG), progettato da David Thomas per l’uso con le GPU tramite OpenCL. Ogni processo di RNG richiede solo due word da 32 bit per la memorizzazione e impiega cinque o sei istruzioni. Inoltre, le istruzioni utilizzate da MWC64X sono supportate da tutte le GPU ad alte prestazioni (i.e. AMD e NVIDIA).

3.6.1 Caratteristiche

Essendo un generatore deterministico, MWC64X utilizza una funzione di transizione di stato, che opera su uno stato a dimensione finita, quindi produce una sequenza pseudo-casuale che si ripete con un periodo costante pari a 2⁶³.
La questione della ripetizione è critica poiché, a causa delle stesse sequenze di valori in ingresso, potrebbe portare a risultati inaspettati in molte applicazioni (ad esempio, qualora vi fossero parecchie GPU in parallelo o le simulazioni durassero giorni). Inoltre, MWC64X è basato sul Multiply With Carry, un RNG a qualità teorica e periodo noti, opportunamente modificato per migliorare la qualità empirica.

4. Implementazione sequenziale

Nella versione sequenziale, il codice per la simulazione di ogni modello si trova in un unico file .py.

4.1 Diffusione delle epidemie

L’algoritmo di “disease spreading”, nell’implementazione sequenziale, è contenuto nella funzione sequential_disease_spreading (invocata dal __main__) e, ∀ t ∈ [0, T], consiste nelle seguenti fasi:
1) Aggiornamento degli stati x(t).
2) Aggiornamento delle posizioni y(t).
3) Aggiunta di n_I(t) al grafico degli agenti infetti.
4) Controllo sul numero di agenti infetti: se n_I(t) = 0, interruzione del ciclo.

4.1.1 sequential_disease_spreading.py

Librerie
Importiamo le librerie necessarie: math (per eseguire funzioni matematiche), matplotlib.pyplot, numpy, random (per generare numeri casuali) e time (per calcolare il tempo di esecuzione).

import math, matplotlib.pyplot, numpy, random, time

Costanti
Definiamo le costanti: S, I e R, corrispondenti ai tre stati del modello SIR, suscettibile, infetto e guarito.

S = 0
I = 1
R = 2

Variabili di ingresso
Definiamo le variabili di ingresso: il numero di agenti n, la densità Ρ, il numero massimo di passi temporali T, la probabilità di salto pJ, il raggio di interazione r, la velocità v, la percentuale di agenti infetti qI, la probabilità che un agente suscettibile contragga l’infezione pIe la probabilità che un agente infetto guarisca pR.

n = 250
Ρ = [0.1, 0.5, 1.0, 5.0, 10.0]
T = 250
pJ = 0.01
r = 1.0
v = 0.1
qI = 0.1
pI = 0.1
pR = 0.05

Variabili di uscita
Definiamo le variabili di uscita: la dimensione del piano l, il numero di agenti infetti nI, gli stati attuali x e temporanei x0, e le posizioni y.

l = None
nI = None
x = numpy.ndarray(n, dtype = numpy.uint32)
x0 = numpy.ndarray(n, dtype = numpy.uint32)
y = numpy.ndarray((n, 2), dtype = numpy.float32)

Variabili del grafico
Definiamo le variabili del grafico: la lista degli istanti temporali wt, la lista dei numeri di agenti infetti wnI e la lista delle etichette wz.

wt = list(list())
wnI = list(list())
wz = list()

Funzioni di supporto
Definiamo le funzioni di supporto: print_config e get_d.

La funzione print_config stampa la configurazione della rete.

def print_config():
  # …

La funzione get_d restituisce la distanza tra due posizioni, y1 e y2.

def get_d(y1, y2):
  d = y1 − y2
  if d[0] < −l / 2:
    d[0] += l
  elif d[0] >= l / 2:
    d[0] −= l
  if d[1] < −l / 2:
    d[1] += l
  elif d[1] >= l / 2:
    d[1] −= l
  return pow(pow(d[0], 2) + pow(d[1], 2), 0.5)

Funzione di simulazione sequenziale
Definiamo la funzione di simulazione sequenziale sequential_disease_spreading, che simula – in maniera sequenziale – il modello di diffusione delle epidemie.

def sequential_disease_spreading(ρ):
  # specifichiamo che le variabili l, nI e x sono globali
  global l
  global nI
  global x
  # impostiamo i valori iniziali di l, nI, x e y
  l = pow(n / ρ, 0.5)
  nI = int(n * qI)
  x[:nI] = I
  x[nI:] = S
  for i in range:
    y[i, 0] = random.uniform(−l / 2, l / 2)
    y[i, 1] = random.uniform(−l / 2, l / 2)
  # aggiungiamo una lista vuota a wt e wnI
  wt.append(list())
  wnI.append(list())
  # definiamo l'indice o, che rappresenta la posizione attuale nella lista
  o = Ρ.index(ρ)
  print " ", o + 1, " of ", len(Ρ)
  # adesso esaminiamo la parte di codice che verrà iterata per ogni istante temporale t
  for t in range(T):
    # 1) aggiorniamo gli stati x
    for i in range(n):
      x0[i] = x[i]
      if x[i] == S:
        mI = 0
        for j in range(n):
          if i != j and x[j] == I and get_d(y[i], y[j]) < r:
            mI += 1
        if random.random() < 1.0 - pow(1.0 - pI, mI):
          x0[i] = I
          nI += 1 
      elif x[i] == I:
        if random.random() < pR:
          x0[i] = R
          nI -= 1
    x = x0
    # 2) aggiorniamo le posizioni y
    for i in range(n):
      if pJ != 0.0 and random.random() < pJ:
        y[i][0] = random.uniform(-l / 2, l / 2)
        y[i][1] = random.uniform(-l / 2, l / 2)
      else:
        θ = random.uniform(-math.pi, math.pi)
        y[i][0] += v * math.cos(θ)
        y[i][1] += v * math.sin(θ)
        while y[i][0] < -l / 2:
          y[i][0] += l
        while y[i][0] >= l / 2:
          y[i][0] -= l
        while y[i][1] < -l / 2:
          y[i][1] += l
        while y[i][1] >= l / 2:
          y[i][1] -= l
    # 3) aggiungiamo t e nI alla posizione o-esima delle liste wt e wnI
    wt[o].append(t)
    wnI[o].append(nI)
    # 4) se nessun agente è infetto, interrompiamo il ciclo 
    if nI == 0:
      break

Funzione main
La funzione __main__ chiama sequential_disease_spreading al variare di ogni ρ in Ρ, stampa il tempo impiegato dalla simulazione e, infine, mostra il grafico del numero di agenti infetti per ogni istante.

if __name__ == "__main__":
  print_config()
  t1 = time.time()
  print "Simulation:"
  for ρ in Ρ:
    sequential_disease_spreading(ρ)
    o = Ρ.index(ρ)
    wz.append(matplotlib.pyplot.plot(wt[o], wnI[o]))
  matplotlib.pyplot.axis([0, T, 0, n])
  matplotlib.pyplot.figlegend(wz, Ρ, 'upper right')
  t2 = time.time()
  print "Elapsed time: ", t2 − t1, "s"
  matplotlib.pyplot.show()

4.2 Evoluzione della cooperazione

L’algoritmo di “evolution of cooperation”, nell’implementazione sequenziale, è contenuto nella funzione sequential_cooperation_evolution (invocata dal __main__) e, ∀ t ∈ [0, T], consiste nelle seguenti fasi:
1) Aggiornamento delle strategie x(t).
2) Aggiornamento delle posizioni y(t).
3) Aggiornamento dei guadagni g(t) e del numero di agenti vicini m(t).
4) Aggiunta di n_C(t) al grafico degli agenti cooperatori.
5) Controllo sul numero di agenti cooperatori: se n_C(t) = 0 oppure n_C(t) = n, interruzione del ciclo.

4.2.1 sequential_cooperation_evolution.py

Librerie
Importiamo le librerie necessarie: math (per eseguire funzioni matematiche), matplotlib.pyplot, numpy, random (per generare numeri casuali) e time (per calcolare il tempo di esecuzione).

import math, matplotlib.pyplot, numpy, random, time

Costanti
Definiamo le costanti: D e C, corrispondenti alle due strategie del dilemma del prigioniero, diserzione e cooperazione.

D = 0
C = 1

Variabili di ingresso
Definiamo le variabili di ingresso: il numero di agenti n, la densità Ρ, il numero massimo di passi temporali T, la probabilità di salto pJ, il raggio di interazione r, la velocità v, la probabilità che un agente cooperi pC e i guadagni nelle quattro situazioni possibili gDC, gCC, gDD e gCD (parametri del modello).

n = 250
Ρ = [0.1, 0.5, 1.0, 5.0, 10.0]
T = 1000
pJ = 0.0
r = 1.0
v = 0.1
pC = 0.5
gDC = 1.1
gCC = 1.0
gDD = 0.0
gCD = 0.0

Variabili di uscita
Definiamo le variabili di uscita: la dimensione del piano l, il numero di agenti cooperatori nC, le strategie attuali x e temporanee x0, le posizioni y, i guadagni g e i numeri dei vicini m.

l = None
nC = None
x = numpy.ndarray(n, dtype = numpy.uint32)
x0 = numpy.ndarray(n, dtype = numpy.uint32)
y = numpy.ndarray((n, 2), dtype = numpy.float32)
g = numpy.ndarray(n, dtype = numpy.uint32)
m = numpy.ndarray(n, dtype = numpy.uint32)

Variabili del grafico
Definiamo le variabili del grafico: la lista degli istanti temporali wt, la lista dei numeri di agenti cooperatori wnC e la lista delle etichette wz.

wt = list(list())
wnC = list(list())
wz = list()

Funzioni di supporto
Definiamo le funzioni di supporto: print_config, get_d, get_max e get_g.

La funzione print_config stampa la configurazione della rete.

def print_config():
  # …

La funzione get_d restituisce la distanza tra due posizioni, y1 e y2.

def get_d(y1, y2):
  d = y1 − y2
  if d[0] < −l / 2:
    d[0] += l
  elif d[0] >= l / 2:
    d[0] −= l
  if d[1] < −l / 2:
    d[1] += l
  elif d[1] >= l / 2:
    d[1] −= l
  return pow(pow(d[0], 2) + pow(d[1], 2), 0.5)

La funzione get_max restituisce il massimo tra due valori, m1 e m2.

def get_max(m1, m2):
  if m1 > m2:
    return m1
  else:
    return m2

La funzione get_g restituisce il guadagno di un agente, in funzione di due strategie, x1 e x2.

def get_g(x1, x2):
  if x1 == D and x2 == C:
    return gDC
  elif x1 == C and x2 == C:
    return gCC
  elif x1 == D and x2 == D:
    return gDD
  else:
    return gCD

Funzione di simulazione sequenziale
Definiamo la funzione sequential_cooperation_evolution, che simula – in maniera sequenziale – il processo di evoluzione della cooperazione.

def sequential_cooperation_evolution(ρ):
  # specifichiamo che le variabili l, n_C e x sono globali
  global l
  global nC
  global x
  # impostiamo i valori iniziali di l, nC, x, y, g e m
  l = pow(n / ρ, 0.5)
  nC = 0
  for i in range(n):
    if random.random() < p_C:
      x[i] = C
    else:
      x[i] = D
  for i in range(n):
    y[i, 0] = random.uniform(-l / 2, l / 2)
    y[i, 1] = random.uniform(-l / 2, l / 2)
  g[:] = 0.0
  m[:] = 0
  # aggiungiamo una lista vuota a wt e wnC
  wt.append(list())
  wnC.append(list())
  # definiamo l'indice o, che rappresenta la posizione attuale nella lista
  o = Ρ.index(ρ)
  print " ", o + 1, " of ", len(Ρ)
  # adesso esaminiamo la parte di codice che verrà iterata per ogni istante temporale t
  for t in range(T):
    # 1) aggiorniamo le strategie x
    for i in range(n):
      x0[i] = x[i]
      if m[i] > 0:
        for j in range (n):
          if i != j and get_d(y[i], y[j]) < r:
            if g[i] < g[j]:
              if random.random() < (g[j] - g[i]) / (get_max(m[i], m[j]) * gDC):
                x0[i] = x[j]
              break
            else:
              break
    x = x0
    # 2) aggiorniamo le posizioni y
    for i in range(n):
      if pJ != 0.0 and random.random() < pJ:
        y[i][0] = random.uniform(-l / 2, l / 2)
        y[i][1] = random.uniform(-l / 2, l / 2)
      else:
        θ = random.uniform(-math.pi, math.pi)
        y[i][0] += v * math.cos(θ)
        y[i][1] += v * math.sin(θ)
        while y[i][0] < -l / 2:
          y[i][0] += l
        while y[i][0] >= l / 2:
          y[i][0] -= l
        while y[i][1] < -l / 2:
          y[i][1] += l
        while y[i][1] >= l / 2:
          y[i][1] -= l
    # 3) aggiorniamo i guadagni g e il numero di agenti vicini m
    for i in range(n):
      g[i] = 0.0 # questa istruzione va commentata per iterare il gioco
      m[i] = 0
      for j in range(n):
        if i != j and get_d(y[i], y[j]) < r:
          g[i] += get_g(x[i], x[j])
          m[i] += 1
    # 4) aggiorniamo il numero di agenti cooperatori nC
    nC = x.sum()
    # 5) aggiungiamo t e nI alla posizione o-esima delle liste wt e wnC
    wt[o].append(t)
    wnC[o].append(nC)
    if nC == 0 or nC == n:
      break

Funzione main
La funzione __main__ chiama sequential_cooperation_evolution al variare di ogni ρ in Ρ, stampa il tempo impiegato dalla simulazione e, infine, mostra il grafico del numero di agenti cooperatori per ogni istante.

if __name__ == "__main__":
  print_config()
  t1 = time.time()
  print "Simulation:"
  for ρ in Ρ:
    sequential_cooperation_evolution(ρ)
    o = Ρ.index(ρ)
    wz.append(matplotlib.pyplot.plot(wt[o], wnC[o]))
  matplotlib.pyplot.axis([0, T, 0, n])
  matplotlib.pyplot.figlegend(wz, Ρ, 'upper right')
  t2 = time.time()
  print "Elapsed time: ", t2 − t1, "s"
  matplotlib.pyplot.show()

4.3 Sincronizzazione del caos

L’algoritmo di “synchronization of chaos”, nell’implementazione sequenziale, è contenuto nella funzione sequential_chaos_synchronization (invocata dal __main__) e, ∀ t ∈ [0, T], consiste nelle seguenti fasi:
1) Aggiornamento degli stati x(t).
2) Aggiornamento delle posizioni y(t).
3) Aggiornamento dell’errore di sincronizzazione e(t).

4.3.1 sequential_chaos_synchronization.py

Librerie
Importiamo le librerie necessarie: math (per eseguire funzioni matematiche), matplotlib.pyplot, numpy, random (per generare numeri casuali), scipy (per utilizzare i passi di integrazione) e time (per calcolare il tempo di esecuzione).

import math, matplotlib.pyplot, numpy, random, scipy, time

Variabili di ingresso
Definiamo le variabili di ingresso: il numero di agenti n, la densità Ρ, il numero massimo di passi temporali T, la durata di ogni passo Δt, la probabilità di salto pJ, il raggio di interazione r, la velocità v, il coefficiente di accoppiamento k e le costanti a, b e c.

n = 2
Ρ = [0.001, 0.005, 0.01, 0.05, 0.1]
T = 500.0
Δt = 0.001
pJ = 0.0
r = 1.0
v = 1.0
k = 10.0
a = 0.2
b = 0.2
c = 7.0

Variabili di uscita
Definiamo le variabili di uscita: la dimensione del piano l, l’errore di sincronizzazione e, l’indice di sincronizzazione δ e strategie attuali x e temporanee x0, le posizioni y, i guadagni g e i numeri dei vicini m.

l = None
e = None
δ = None
x = numpy.ndarray((n, 3), dtype = numpy.float32)
x0 = numpy.ndarray((n, 3), dtype = numpy.float32)
y = numpy.ndarray((n, 2), dtype = numpy.float32)

Variabili del grafico
Definiamo le variabili del grafico: la lista delle densità wρ e la lista degli indici di sincronizzazione wδ.

wρ = list()
wδ = list()

Funzioni di supporto
Definiamo le funzioni di supporto: print_config e get_d.

La funzione print_config stampa la configurazione della rete.

def print_config():
  # …

La funzione get_d restituisce la distanza tra due posizioni, y1 e y2.

def get_d(y1, y2):
  d = y1 − y2
  if d[0] < −l / 2:
    d[0] += l
  elif d[0] >= l / 2:
    d[0] −= l
  if d[1] < −l / 2:
    d[1] += l
  elif d[1] >= l / 2:
    d[1] −= l
  return pow(pow(d[0], 2) + pow(d[1], 2), 0.5)

Funzione di simulazione sequenziale
Definiamo la funzione sequential_chaos_synchronization, che simula – in maniera sequenziale – il meccanismo di sincronizzazione del caos.

⚠️

Funzione main
La funzione __main__ chiama sequential_chaos_synchronization al variare di ogni ρ in Ρ, stampa il tempo impiegato dalla simulazione e, infine, mostra il grafico dell’indice di sincronizzazione per ogni densità.

if __name__ == "__main__":
  print_config()
  t1 = time.time()
  print "Simulation:"
  for ρ in Ρ:
    sequential_chaos_synchronization(ρ)
  matplotlib.pyplot.plot(wρ, wδ)
  t2 = time.time()
  print "Elapsed time: ", t2 − t1, "s"
  matplotlib.pyplot.show()

5. Implementazione parallela

Nella versione parallela, il codice per la simulazione di ogni modello è distribuito su due file: l’host .py e il kernel .cl.

5.1 Diffusione delle epidemie

L’algoritmo di “disease spreading”, nell’implementazione parallela, è contenuto nella funzione host parallel_disease_spreading (invocata dal __main__) e, ∀ t ∈ [0, T], consiste nelle seguenti fasi:
1) Invocazione della funzione kernel parallel_disease_spreading.
2) Copia del contenuto del buffer Ln_I,out(t) in Ln_I(t).
3) Calcolo del numero globale di agenti infetti n_I(t).
4) Aggiunta di n_I(t) al grafico degli agenti infetti.
5) Controllo sul numero di agenti infetti: se n_I = 0, interruzione del ciclo.
La funzione kernel, ∀ t ∈ [0, T] e ∀ i ∈ {1, …, n}, esegue i seguenti passi:
1) Aggiornamento dello stato x_i,out(t).
2) Aggiornamento della posizione y_i,out(t).
3) Se Li = 0, aggiornamento del numero locale di agenti infetti Ln_I,out(t).

5.1.1 parallel_disease_spreading.py (host)

⚠️

5.1.2 parallel_disease_spreading.cl (kernel)

⚠️

5.2 Evoluzione della cooperazione

⚠️

5.3 Sincronizzazione del caos

⚠️

6. Valutazioni

Tutti i test riportati in questo capitolo sono stati effettuati su un computer Apple MacBook Pro 8.2 (Early 2011) con processore quad-core Intel Core i7 “Sandy Bridge” a 2.0 GHz (con 6 MB di cache L3 condivisa), 8 GB di memoria DDR3 a 1333 MHz, scheda video integrata Intel Graphics 3000 (con 384 MB di memoria DDR3) e dedicata AMD Radeon HD 6490M (con 256 MB di memoria GDDR5), e sistema operativo Mac OS X Snow Leopard (versione 10.6.8).
I test sono stati orientati a verificare l’effettivo funzionamento delle routine implementate (confrontando i loro risultati con quelli riportati in letteratura) e le performance delle versioni sequenziali e parallele.

6.1 Diffusione delle epidemie

6.1.1 Risultati

In generale, durante ogni simulazione del processo di diffusione delle malattie, il numero di individui infetti n_I (t) segue un andamento stereotipato: aumenta, raggiunge un valore di picco, quindi decresce.
Una situazione tipica è mostrata nella figura 6.1: il picco di individui infetti (ed, analogamente, il numero complessivo di individui che hanno contratto la malattia alla fine del processo) è più alto nei casi in cui la densità è maggiore; anche un aumento della probabilità di salto (figura 6.2) e della velocità (figura 6.3) favorisce la diffusione dell’epidemia.

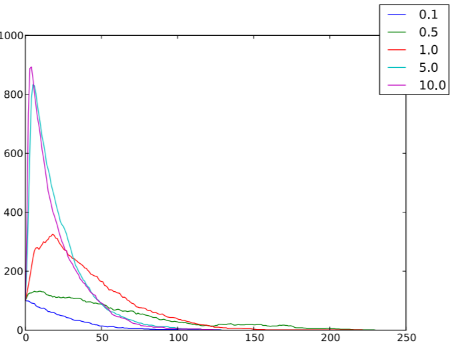
Figura 6.1: Numero di individui infetti n_I per ogni istante temporale t, al variare delle densità ρ ∈ {0.1, 0.5, 1, 5, 10}, in un sistema caratterizzato da n = 1000, T = 250, q_I = 0.1, p_J = 0.01, r = 1, v = 0.1, p_I = 0.1 e p_R = 0.05.

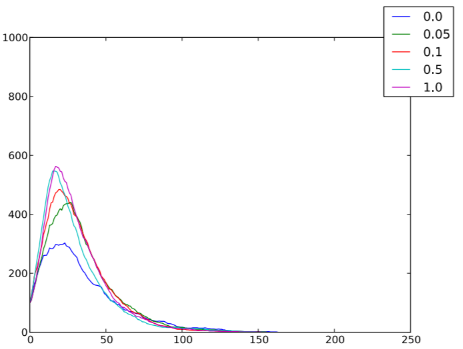
Figura 6.2: Numero di individui infetti n_I per ogni istante temporale t, al variare delle probabilità di salto p_J ∈ {0, 0.05, 0.1, 0.5, 1}, in un sistema caratterizzato da n = 1000, ρ = 1, T = 250, q_I = 0.1, r = 1, v = 0.1, p_I = 0.1 e p_R = 0.05.

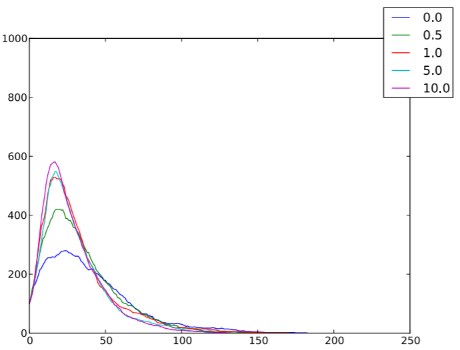
Figura 6.3: Numero di individui infetti n_I per ogni istante temporale t, al variare delle velocità v ∈ {0.1, 0.5, 1, 5, 10}, in un sistema caratterizzato da n = 1000, ρ = 1, T = 250, q_I = 0.1, p_J = 0.01, r = 1, p_I = 0.1 e p_R = 0.05.

6.1.2 Tempi di esecuzione

Nella tabella 6.1 sono registrati i tempi medi di esecuzione di entrambe le implementazioni del simulatore “disease spreading”. Si può notare che, all’aumentare del numero di agenti n, i tempi di esecuzione della versione parallela sono nettamente inferiori, rispetto a quelli della versione sequenziale.

n	Δ TΣ [s]	nL	Δ TΠ [s]
10	0.2	10	0.6
25	0.5	25	0.6
50	2.0	50	0.7
100	6.7	100	0.7
250	39	250	0.9
500	159	250	1.1
1000	667	250	1.5
2500	3958	250	3.7
5000	…	250	9.4
10000	…	250	26
25000	…	250	129

Tabella 6.1: Tempi di esecuzione della versione sequenziale Δ T_Σ e parallela Δ T_Π (valori medi calcolati su 10 differenti realizzazioni) del simulatore “disease spreading”, al variare del numero globale n e locale n_L di agenti, in un sistema caratterizzato da ρ = 1, T = 250, q_I = 0.1, p_J = 0.01, r = 1, v = 0.1, p_I = 0.1 e p_R = 0.05.

6.2 Evoluzione della cooperazione

6.2.1 Risultati

Simulando il meccanismo di evoluzione della cooperazione, la scelta della strategia finale dipende dai parametri di ingresso.
Ad esempio, la densità degli agenti (figura 6.4), la probabilità di salto (figura 6.5), la velocità (figura 6.6) e i valori dei guadagni (figura 6.7) influenzano la strategia adottata dal sistema a regime.

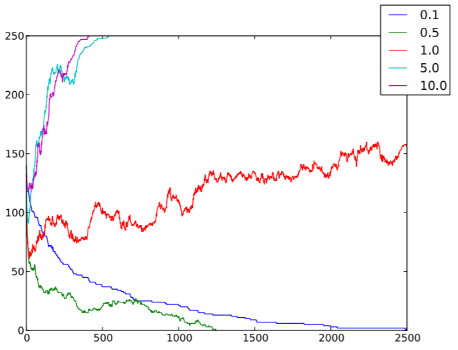
Figura 6.4: Numero di individui cooperatori n_C per ogni istante temporale t, al variare delle densità ρ ∈ {0.1, 0.5, 1, 5, 10}, in un sistema caratterizzato da n = 250, T = 2500, p_C = 0.5, p_J = 0, r = 1, v = 0.1, g_DC = 1.1, g_CC = 1, g_DD = 0 e g_CD = 0.

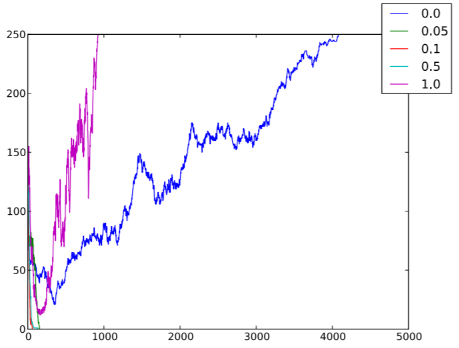
Figura 6.5: Numero di individui cooperatori n_C per ogni istante temporale t, al variare delle probabilità di salto p_J ∈ {0, 0.05, 0.1, 0.5, 1}, in un sistema caratterizzato da n = 250, ρ = 1, T = 5000, p_C = 0.5, r = 1, v = 0.1, g_DC = 1.1, g_CC = 1, g_DD = 0 e g_CD = 0.

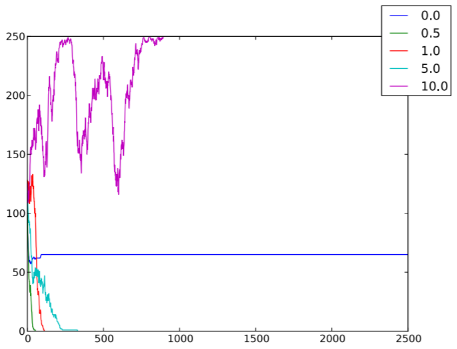
Figura 6.6: Numero di individui cooperatori n_C per ogni istante temporale t, al variare delle velocità v ∈ {0, 0.05, 0.1, 0.5, 1}, in un sistema caratterizzato da n = 250, ρ = 1, T = 2500, p_C = 0.5, p_J = 0, r = 1, g_DC = 1.1, g_CC = 1, g_DD = 0 e g_CD = 0.

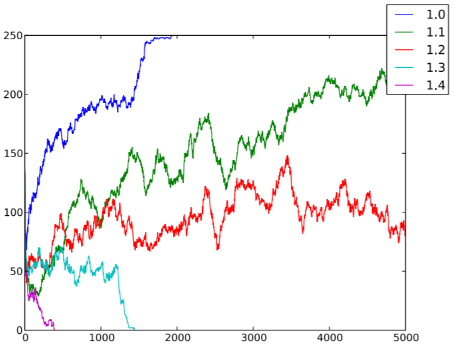
Figura 6.7: Numero di individui cooperatori n_C per ogni istante temporale t, al variare dei guadagni g_DC ∈ {1, 1.1, 1.2, 1.3, 1.4}, in un sistema caratterizzato da n = 250, T = 5000, p_C = 0.5, p_J = 0, r = 1, v = 0.1, g_CC = 1, g_DD = 0 e g_CD = 0.

6.2.2 Tempi di esecuzione

Nella tabella 6.2 sono registrati i tempi medi di esecuzione di entrambe le implementazioni del simulatore “evolution of cooperation”.
Si può notare che, all’aumentare del numero di agenti n, i tempi di esecuzione della versione parallela sono nettamente inferiori, rispetto a quelli della versione sequenziale.

n	Δ TΣ [s]	nL	Δ TΠ [s]
10	0.5	10	0.5
25	3.4	25	1.2
50	31	50	2.3
100	269	100	3.2
250	1848	250	5.4
500	4429	250	7.0
1000	…	250	12
2500	…	250	51
5000	…	250	173

Tabella 6.2: Tempi di esecuzione della versione sequenziale Δ T_Σ e parallela Δ T_Π (valori medi calcolati su 10 differenti realizzazioni) del simulatore “evolution of cooperation”, al variare del numero globale n e locale n_L di agenti, in un sistema caratterizzato da ρ = 1, T = 1000, p_C = 0.5, p_J = 0, r = 1, v = 0.1, g_DC = 1.1, g_CC = 1, g_DD = 0 e g_CD = 0.

6.3 Sincronizzazione del caos

6.3.1 Risultati

Per valori di densità ρ₁ < ρ < ρ₂, l’indice δ è zero: ciò corrisponde a una sincronizzazione completa.
Nella figura 6.8 possiamo osservare che i valori critici della densità, ρ₁ e ρ₂, sono indipendenti dal numero degli agenti n, quindi la dimensione reale del sistema non si misura con n, bensì con ρ.

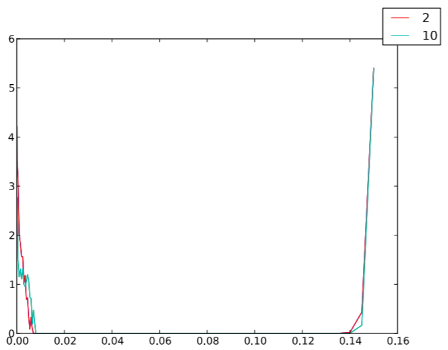
Figura 6.8: Indici di sincronizzazione δ (valori medi calcolati su 10 differenti realizzazioni) per ogni densità ρ, al variare di n ∈ {2, 10}, in un sistema caratterizzato da T = 500, Δt = 0.001, p_J = 0, r = 1, v = 1, k = 10, a = 0.2, b = 0.2 e c = 7.

6.3.2 Tempi di esecuzione

Nella tabella 6.3 sono registrati i tempi medi di esecuzione di entrambe le implementazioni del simulatore “synchronization of chaos”.
Si può notare che, all’aumentare del numero di agenti n, i tempi di esecuzione della versione parallela sono nettamente inferiori, rispetto a quelli della versione sequenziale.

n	Δ TΣ [s]	nL	Δ TΠ [s]
2	0.4	2	3.0
10	6.2	10	3.1
25	37	25	3.2
50	145	100	3.3
100	537	250	3.5
250	3345	250	4.2
500	…	250	5.0
1000	…	250	8.5
2500	…	250	30
5000	…	250	96

Tabella 6.3: Tempi di esecuzione della versione sequenziale Δ T_Σ e parallela Δ T_Π (valori medi calcolati su 10 differenti realizzazioni) del simulatore “synchronization of chaos”, al variare del numero globale n e locale n_L di agenti, in un sistema caratterizzato da ρ = 0.01, T = 1, Δ t = 0.001, p_J = 0, r = 1, v = 1, k = 10, a = 0.2, b = 0.2 e c = 7.

7. Conclusioni

In conclusione, in questa tesi di laurea, abbiamo descritto teoricamente tre modelli ad agenti mobili: la diffusione delle epidemie, l’evoluzione della cooperazione e la sincronizzazione del caos.
Abbiamo realizzato un framework per la simulazione dei suddetti modelli, di cui sono state implementate una versione sequenziale (in Python) e una parallela (in Python e OpenCL).
Quindi, abbiamo rilevato che un aumento della densità (figura 6.1), della probabilità di salto (figura 6.2) oppure della velocità (figura 6.3) favorisce la diffusione dell’epidemia.
Abbiamo studiato gli effetti della mobilità in una popolazione di individui che giocano al dilemma del prigioniero: il sistema tende a diventare cooperativo solo quando la tentazione a disertare (figura 6.7) e la velocità (figura 6.6) degli agenti non sono troppo alte.
Abbiamo dimostrato che un parametro critico per la sincronizzazione di un gruppo di agenti mobili è la densità (figura 6.8): quando è mantenuta costante, il comportamento è indipendente dal numero degli agenti.
Inoltre, dai dati ricavati dalle simulazioni (tabelle 6.1, 6.2 e 6.3), abbiamo osservato che l’implementazione parallela del framework, eseguendo un’elevata quantità di calcoli in parallelo tramite OpenCL, diminuisce notevolmente i tempi di esecuzione, rispetto alla versione sequenziale.
Il codice proposto si può facilmente generalizzare per la simulazione di altri modelli di sistemi complessi ad agenti mobili, sia nel caso in cui si considerino altri tipi di dinamiche associate ad ogni agente, sia nel caso di altri modelli di movimentazione.
Infatti, in questi casi, il nostro framework fornisce routine e procedure facilmente riutilizzabili.