Alessio Cantarella, a cura di Corrado Santoro (relatore), Facoltà di Ingegneria, Università degli Studi di Catania, a.a. 2006/2007

1. Introduzione
La presente tesi di laurea verte sull’analisi di una rete grid a contenuti distribuiti (CDG), nella quale è implementato un algoritmo, per la gestione delle risorse, simile al modello economico di “domanda e offerta” e basato sulla teoria dei giochi.
La scelta di questa implementazione, che deriva dal contesto competitivo in cui si trova tale rete (l’acquisto di una risorsa prevede un costo), risulta la soluzione più indicata per descrivere il meccanismo di contrattazione fra le parti in gioco.
Nei primi capitoli, verrà fornita una breve introduzione della rete, del modello economico utilizzato e della teoria dei giochi, necessaria per comprendere l’algoritmo utilizzato.
Successivamente, si passerà alla descrizione del simulatore, appositamente implementato per studiare la rete, ed alla valutazione dei dati statistici ottenuti, per trarre delle conclusioni sui vantaggi di quest’implementazione.
2. CDN e CDG
Una rete di calcolatori, in generale, è un sistema che permette la condivisione e la distribuzione di informazioni e risorse, sia hardware che software, tra differenti nodi.
Ogni nodo, trovandosi in uno scenario web, può contenere al suo interno tre differenti tipi di risorse:
• disk space (spazio su disco);
• network bandwidth (ampiezza di banda della rete);
• CPU time (tempo di CPU).
2.1 CDN
Una CDN – acronimo di content delivery network (rete a contenuti distribuiti) – è una particolare tipologia di rete caratterizzata da un unico nodo principale (origin server), che duplica le risorse ad un numero imprecisato di nodi secondari (replica server), i quali, a loro volta, le forniscono ai nodi (client), che ne hanno fatto richiesta.
Questa struttura garantisce al sistema, anche in caso di eventuali guasti, di poter recuperare la stessa risorsa da un qualsiasi server funzionante e, soprattutto, tempi più brevi, scegliendo per la trasmissione il server più vicino al client richiedente oppure quello con un minor carico di lavoro (load average).
Occorre precisare che la “vicinanza” fra due nodi non dipende soltanto dalla loro distanza spaziale, ma anche dalla qualità del canale di comunicazione utilizzato (in termini di larghezza di banda), dalla velocità computazionale dei replica server e da altri fattori secondari.
Un’ulteriore peculiarità di una CDN è che tutti i suoi nodi appartengono alla stessa organizzazione, pertanto non vi può essere competitività all’interno di tale rete.
2.1.1 Workflow di esempio
Un esempio di funzionamento di una CDN è il seguente:
1) un client richiede una risorsa (ad esempio: una pagina web con contenuto multimediale) alla CDN;
2) l’origin server determina il replica server più vicino al client e gli ridireziona la richiesta;
3) il replica server fornisce la risorsa al client.
2.2 CDG
Una CDG – acronimo di content delivery grid (grid a contenuti distribuiti) – è un’altra particolare tipologia di rete costituita da un insieme di CDN associate fra loro, ognuna delle quali, sotto opportune condizioni, può richiedere il controllo di un nodo che non le appartiene.
Questa caratteristica risulta essenziale per comprendere il passaggio dal contesto cooperativo di una CDN a quello competitivo di una CDG.
Dunque, in una CDG, un origin server non è vincolato a fornire le risorse mediante uno dei propri replica server, ma può farlo anche attraverso uno appartenente ad un’altra CDN, qualora sia più vicino al client richiedente.
L’utilizzo del replica server da parte dell’origin server avviene tramite una fase di negoziazione, tra le due CDN coinvolte, in cui si cerca di stabilire un prezzo.
Se tale fase andasse a buon fine, il replica server passerebbe temporaneamente sotto il controllo dell’origin server.
L’idea dei grid è scaturita dalla constatazione che, in media, l’utilizzo delle risorse informatiche di una organizzazione è pari al 5% della sua reale potenzialità. Le risorse necessarie sarebbero messe a disposizione da varie entità in modo da creare un’organizzazione virtuale, con a disposizione un’infrastruttura migliore di quella che la singola entità potrebbe sostenere.
2.2.1 Workflow di esempio
⚠️
3. Modello economico
Dallo scenario precedentemente illustrato si comprendono le necessità di utilizzare un algoritmo per favorire la negoziazione fra le due parti e di considerare la risorsa scambiata come se fosse una merce acquistabile o vendibile, utilizzando un certo numero di crediti (¤).
Assumendo che, inizialmente, tutti gli origin server delle CDN appartenenti alla CDG abbiano un certo numero di crediti a disposizione: se quello acquirente (appartenente alla CDN B) possedesse KB ¤ ed il venditore (appartenente alla CDN S) KS ¤, e la risorsa costasse P ¤, alla fine della transazione, il bilancio sarebbe di KB – P ¤ per l’origin server B e di KB + P ¤ per l’origin server S.
Poiché l’obiettivo delle singole CDN è amministrare il proprio ammontare di crediti, nel modo più fruttuoso possibile, si è scelto di implementare un algoritmo simile al modello economico di “domanda e offerta”.
3.1 Curva di domanda
La curva di domanda rappresenta la quantità di crediti che il compratore è disposto a spendere per la risorsa, al variare della quantità da acquistare.
3.2 Curva di offerta
La curva di offerta, invece, rappresenta il prezzo della risorsa (stabilito dal venditore), al variare della quantità da vendere.
3.3 Casi possibili
L’andamento delle due curve è stabilito considerando che le risorse sono limitate, quindi, maggiore è la quantità richiesta, maggiore sarà il prezzo da pagare.
Esso può essere influenzato anche da altri parametri (ad esempio: l’esito delle precedenti negoziazioni con lo stesso origin server).
Se, alla quantità Q di risorsa da scambiare, le due curve si incontrassero in un punto E (punto di equilibrio), l’acquirente ed il venditore si accorderebbero al prezzo P corrispondente.
Ad ogni modo, questa situazione è poco comune, poiché, alla quantità Q, le curve, a meno che non siano uguali, non è detto che coincidano.
Di conseguenza, possiamo distinguere due casi:
• se, alla quantità Q, la curva di domanda sta al di sopra della curva di offerta, la situazione è favorevole per entrambi, specialmente per l’acquirente, che può comprare al prezzo stabilito dal venditore;
• se, invece, alla quantità Q, la curva di domanda sta al di sotto della curva di offerta, affinché sia possibile portare a termine la negoziazione, si tenta di modificare le curve (o almeno una delle due) attraverso un algoritmo, basato sulla teoria dei giochi.
4. Teoria dei giochi
La vita ci costringe continuamente a fare scelte, ad ogni livello (personale, familiare, sociale) ed in ogni campo (morale, economico, politico), in situazioni di conoscenza imperfetta della situazione, del comportamento altrui e degli effetti delle varie scelte.
Nonostante la sua complessità, il processo decisionale può essere comunque modellato con strumenti matematici, nella maniera tipica della scienza: astraendo cioè dalle situazioni reali elementi significativi che si prestino ad un trattamento formalizzato.
La branca della matematica che si interessa di tali problemi è la teoria dei giochi, ed il suo nome è emblematico: per giochi, infatti, si possono intendere sia i contenuti della teoria stessa, che i processi da essa modellati.
Mentre la prima interpretazione è espressione di un atteggiamento equilibrato, che vede la matematica e le sue applicazioni come drastiche semplificazioni della realtà, la seconda è invece espressione di un atteggiamento maniacale, che riduce la complessità del mondo alla rigidità del formalismo matematico e scientifico.
Inutile dire che in occidente è stata la seconda alternativa ad avere la meglio, a cominciare da John Von Neumann (il primo grande esponente della teoria dei giochi), per continuare con i ricercatori della “RAND Corporation” (fra i quali John Nash) e per finire con i numeri consiglieri militari, economici e politici del governo statunitense degli ultimi cinquant’anni.
4.1 Giochi di coppia
Le ipotesi che, da un lato, rendono possibile la trattazione matematica ma, dall’altro, l’allontanano dalla realtà delle cose, consistono nel considerare giochi fra giocatori completamente razionali, il cui unico interesse sia vincere, e che abbiano un’informazione perfetta (sia della situazione, che degli effetti delle azioni): è ovvio che, nella vita, gli individui saranno razionali solo in certa misura, potranno avere interessi molteplici ed avranno solo informazioni parziali.
Fatte queste ipotesi, si consideri una situazione in cui due giocatori (A e B) hanno la possibilità di cooperare (C) o non cooperare (N) fra loro, ottenendo un guadagno o una perdita, a seconda del comportamento di entrambi.
Tipiche situazioni di cooperazione sono l’altruismo, la democrazia, il comunismo e l’internazionalismo, mentre tipiche situazioni di non-cooperazione sono l’egoismo, il totalitarismo, il capitalismo ed il nazionalismo.
Un tipico guadagno è ovviamente il denaro ma, poiché non tutto è qualificabile in termini monetari, la teoria presuppone solo una misura astratta di utilità e lascia aperto il problema della sua determinazione, che è complicata dal fatto che l’utilità è variabile nel tempo (ad esempio: col progredire del gioco, si è disposti a rischiare di più).(1)
Infine, l’utile è spesso influenzato dalla storia passata di un individuo, dall’ambiente e dal contesto in cui si gioca, dal tipo di gioco e così via, ed esso può essere anche negativo (ad esempio: quando si partecipa ad una lotteria o si stipula un’assicurazione, si gioca una piccola somma che quasi sicuramente si perderà, con la speranza di fare un grosso guadagno nel primo caso e di evitare una grossa perdita nel secondo).
Il guadagno del primo giocatore si può rappresentare con una tabella del tipo seguente:
| B coopera | B non coopera | |
|---|---|---|
| A coopera | aCC | aCN |
| A non coopera | aNC | aNN |
Tabella 4.1: Guadagno del giocatore A in un gioco di coppia.
Il guadagno del secondo giocatore si può rappresentare con una tabella analoga:
| B coopera | B non coopera | |
|---|---|---|
| A coopera | bCC | bCN |
| A non coopera | bNC | bNN |
Tabella 4.2: Guadagno del giocatore B in un gioco di coppia.
Per comodità, le due tabelle possono essere unificate in una sola:
| B coopera | B non coopera | |
|---|---|---|
| A coopera | aCC, bCC | aCN, bCN |
| A non coopera | aNC, bNC | aNN, bNN |
Tabella 4.3: Guadagno dei giocatori A e B in un gioco di coppia.
La teoria dei giochi cerca, da un lato, di ricondurre situazioni di potenziale confronto (o conflitto) a giochi del tipo precedente e, dall’atro, di determinare il (o, almeno, un) comportamento razionale per i giocatori: la prima fase corrisponde alla costruzione di un modello e la seconda alla sua analisi.
4.2 Equilibrio di Nash
Uno strumento per l’analisi di un gioco è la seguente nozione, introdotta da Von Neumann e perfezionata da Nash: uno stato del gioco è un equilibrio di Nash se esso rappresenta una situazione in cui entrambi i giocatori non hanno recriminazioni da fare, nel senso che, anche sapendo quale sarebbe stato il comportamento dell’altro giocatore, essi si sarebbero comportati nello stesso modo (in altre parole, la situazione non è migliorabile con atti individuali, benché, in generale, possa esserlo con atti collettivi).
È abbastanza ovvio che se uno stato non è di equilibrio, allora non è razionale: almeno un giocatore, in seguito, penserà che avrebbe potuto far meglio.
Quindi, l’equilibrio di Nash costituisce una condizione necessaria per un comportamento razionale, ma il problema è che non costituisce una condizione sufficiente: ci sono giochi in cui l’equilibrio di Nash non è per niente razionale, e in cui l’unico comportamento razionale è quello di non giocare!
4.3 Giochi simmetrici
Un gioco si dice simmetrico se i due giocatori hanno lo stesso guadagno in condizioni analoghe, cioè:
aCC = bCC,
aNN = bNN,
aCN = bNC,
aNC = bCN.
Le prime due condizioni sono ovvie. Per comprendere le altre due, si ricordi che aCN è quel che A guadagna se A collabora e B non collabora, mentre bNC è ciò che B guadagna se A non collabora e B collabora, e quindi in entrambi i casi si ha il guadagno di un giocatore nel caso in cui egli collabora e l’altro no.
Se esiste un comportamento razionale per i due giocatori in un gioco simmetrico, esso deve ovviamente essere lo stesso per entrambi: o tutti collaborano o nessuno collabora.(2)
Fra i giochi simmetrici, particolarmente semplici sono quelli puramente qualitativi, in cui cioè non è l’importo assoluto dei guadagni che conta per i giocatori (nel qual caso, il gioco si direbbe quantitativo), ma solo il loro valore relativo.
Il gioco è allora completamente determinato dal modo in cui i giocatori ordinano le quattro possibilità: CC, CN, NC, NN.
4.4 Dilemma del prigioniero
Il gioco determinato da
NC > CC > NN > CN,
si chiama dilemma del prigioniero, a causa della versione proposta da Albert Tucker,(3) e può essere sintetizzato così:
Due sospetti (A e B) di un crimine dono arrestati ed interrogati separatamente. Viene loro detto che:
• se uno dei due denuncia l’altro, sarà liberato, mentre il complice sarà condannato alla pena intera (dieci anni di carcere);
• se, però, si denunciano a vicenda, allora entrambi saranno condannati ad una pena intermedia (cinque anni di carcere);
• se, invece, nessuno dei due parla, entrambi saranno condannati ad una pena ridotta (un anno di carcere).
Il ragionamento di ciascun giocatore si può riassumere nel seguente modo:
• la migliore ipotesi è che io parli e l’altro no (NC), così che io sarò liberato;
• la seconda migliore ipotesi è che nessuno di noi parli (CC), perché almeno io sarò condannato ad una pena ridotta;
• se, però, l’altro decide di parlare, il meglio è che anch’io parli (NN), perché così almeno prenderò una pena ridotta;
• la peggiore delle ipotesi è che solo l’altro parli (CN), perché allora io sarò condannato all’intera pena.
La tabella del gioco è ora:
| B coopera | B non coopera | |
|---|---|---|
| A coopera | -1, -1 | -10, 0 |
| A non coopera | 0, -10 | -5, -5 |
Tabella 4.4: Guadagno dei giocatori A e B nel dilemma del prigioniero.
In questo caso c’è un solo equilibrio di Nash. Dato un gioco di coppia, la determinazione degli equilibri di Nash si può fare facilmente nel modo seguente.
Si considera la tabella del primo giocatore e si pone in ciascuna colonna (che rappresenta un comportamento fisso del secondo giocatore) una freccia che va dalla possibilità meno favorevole a quella più favorevole (essa rappresenta un possibile miglioramento della strategia del primo giocatore): ci sono solo quattro possibilità, poiché le frecce possono essere rivolte entrambe in alto, entrambe in basso, una in alto ed una in basso o viceversa. Si considera poi la tabella del secondo giocatore e si pone in ciascuna riga (che rappresenta un comportamento fisso del primo giocatore) una freccia analoga (che rappresenta un possibile miglioramento della strategia del secondo giocatore): di nuovo ci sono quattro possibilità. Ponendo insieme le frecce delle due tabelle, gli eventuali punti a cui esse tendono sono gli equilibri di Nash (in grassetto).
| -1 → -10 | -1 → 0 | -1, -1 → -10, 0 |
| ↓ → ↓ | ↓ → ↓ | |
| 0 → -5 | -10 → -5 | 0, -10 → -5, -5 |
Tabella 4.5: Equilibrio di Nash nel dilemma del prigioniero.
Benché esista una sola possibilità, che è simmetrica, ad essa si accompagna comunque un dilemma.
Infatti, da un lato, la non-cooperazione (“non fare agli altri ciò che temi non sarà fatto a te”) è la sola possibilità razionale, dall’altro, la cooperazione (“fai agli altri ciò che speri sia fatto a te”) è però considerata più desiderabile (perché CC > NN).
La non-cooperazione propria è addirittura un comportamento dominante (nel senso che rappresenta una scelta razionale ed ovvia, qualunque sia il comportamento dell’avversario): è meglio per me che io non cooperi, qualunque cosa l’altro faccia. D’altra parte, anche la cooperazione altrui è un comportamento dominante: è meglio per me che l’altro cooperi, qualunque cosa io faccia. Il dilemma deriva dalla simmetria di questo ragionamento, che vale per entrambi i giocatori.
Il dilemma formalizza quindi un conflitto fra razionalità ed interesse, che sembra essere tipico di molte situazioni concrete.
Nel melodramma, il dilemma è stato descritto, ad esempio, nella Tosca (1900) di Giacomo Puccini, il commissario Scarpia ha condannato l’amante di Tosca a morte e le offre di salvarlo in cambio di una notte d’amore. In ordine decrescente di preferenza, Tosca ha le seguenti possibilità: salvare l’amante senza cedere (NC), salvare l’amante cedendo (CC), non salvare l’amante senza però cedere (NN) e non salvare l’amante pur cedendo (CC). Tosca e Scarpia decidono di comportarsi entrambi razionalmente, seguendo l’equilibrio di Nash: lei lo pugnala prima di concederglisi e lui l’ha già tradita, dando l’ordine di fucilare l’amante.
Nella vita reale, il dilemma si presenta ogni volta che non si aiuta il prossimo temendo che esso non aiuterà noi o quando si decide di non fare l’azione giusta temendo che anche gli altri non la faranno. Casi tipici sono le situazioni (politiche, economiche e militari) in cui nessuno dei due contendenti è disposto a fare il primo passo per il raggiungimento di un benessere comune (ad esempio: il disarmo, i negoziati di pace, ecc.) ed i comportamenti sociali che provocherebbero benessere se fossero generalizzati (ad esempio: pagare tangenti, non pagare tasse ed imposte, ecc.).
A scanso di equivoci, è giusto sottolineare che sebbene la cooperazione sia più vantaggiosa per i due giocatori, non lo è necessariamente anche per la società (ad esempio: i cartelli dei prezzi si possono vedere come la scelta di cooperazione fra i venditori, che rinunciano alla competizione per trarre un maggior guadagno collettivo a danno dei consumatori).
4.5 Giochi iterati
Finora si è ragionato come se il gioco fosse giocato una sola volta.
Se, in qualche modo, si vogliono simulare situazioni della vita reale, si dovrà permettere al gioco di essere iterato indefinitivamente: cooperazione e non-cooperazione potranno allora essere alternate, in proporzioni variabili, anche in risposta (positiva o negativa) al comportamento altrui.
4.6 Dilemma del prigioniero iterato
Mentre “non cooperare mai” continua ad essere un equilibrio di Nash per il dilemma del prigioniero iterato, lo diventano anche “cooperare sempre” ed il cosiddetto tit-for-tat(4) che richiede di iniziare con una cooperazione e di continuare ripetendo il comportamento che l’altro giocatore ha tenuto nella giocata precedente.
Che la cooperazione sia un equilibrio di Nash, deriva dal fatto che essa è dominante per il gioco non iterato. Che lo sia anche la non-cooperazione, deriva dal fatto che essa è ciò che si ottiene se entrambi i giocatori giocano “pan per focaccia”. Che lo sia anche quest’ultima deriva dal fatto che non conviene per uno dei giocatori incominciare a non cooperare, per poi eventualmente ritornare a cooperare.
Robert Axelrod organizzò un torneo, basato sul dilemma del prigioniero iterato, in cui i giocatori dovevano, di volta in volta, scegliere una strategia e tenere memoria degli incontri precedenti: l’idea era di studiare un possibile modello evolutivo di schemi comportamentali ed il risultato fu che tit-for-tat divenne la strategia più diffusa del modello.
I motivi sembrerebbero essere molti: la strategia è semplice e persuasiva, non è aggressiva ma neppure passiva, reagisce in modo immediato (subito) e moderato (una sola volta) sia alle provocazioni che ai pentimenti, e non ha bisogna di segretezza.
Anche le conseguenze sembrerebbero essere chiare: la reciprocità è un comportamento evoluzionisticamente vincente.
Eppure, un’analisi teorica rivela che tali considerazioni empiriche possono essere fuorvianti.
Si può infatti calcolare la stabilità evolutiva di un comportamento in un gioco simmetrico immaginando di avere una popolazione i cui giocatori cooperino con probabilità p e, quindi, non cooperino con probabilità 1 – p.
Poiché la capacità di sopravvivenza di un giocatore (A) è misurata dal suo potenziale guadagno, se egli non coopera, essa sarà:
aNC p + aNN (1 – p),
mentre, se egli coopera, essa sarà:
aCC p + aCN (1 – p).
Dunque, la condizione affinché la cooperazione sia evoluzionisticamente vincente è:
aNC p + aNN (1 – p) < aCC p + aCN (1 – p).
Nel caso specifico del dilemma del prigioniero, essa diventa:
0 p + (-5) (1 – p) < (-1) p + (-10) (1 – p),
cioè, invertendo i segni:
5 (1 – p) > p + 10 (1 – p),
che, per p ∈ [0, 1], è una disuguaglianza impossibile.
In altre parole, l’unica condizione di stabilità evolutiva nel dilemma del prigioniero è quella in cui nessuno coopera.
5. Algoritmo di negoziazione
L’algoritmo di negoziazione prova a modificare, di volta in volta, le curve di domanda e di offerta (o almeno una delle due) finché la proposta d’acquisto non è maggiore o uguale al prezzo di vendita.
La negoziazione può essere considerata un gioco iterato, simmetrico e di coppia (simile al dilemma del prigioniero iterato), in cui ognuno dei due giocatori (l’acquirente ed il venditore), di volta in volta, può decidere di cooperare (modificare la sua curva) o no (mantenerla costante).
Quest’ultima scelta, come si vedrà successivamente, è condizionata dall’esito delle precedenti negoziazioni.
5.1 Probabilità contro logica
Paradossalmente, sebbene nel dilemma del prigioniero iterato la non-cooperazione rappresenti lo stato di equilibrio, se tutti e due i giocatori scegliessero tirando una moneta, avrebbero più possibilità di ridurre i loro anni di prigionia, infatti se entrambi non cooperassero, ogni prigioniero avrebbe il 100% di probabilità di essere condannato a cinque anni di carcere. Se, invece, entrambi adottassero una scelta casuale, ogni prigioniero avrebbe:
• il 25% di probabilità di essere condannato a dieci anni di carcere;
• il 25% di probabilità di essere condannato a cinque anni di carcere;
• il 25% di probabilità di essere condannato a un anno di carcere;
• il 25% di probabilità di essere libero.
Nella scelta con le monete, chiaramente, la situazione è migliore per entrambi, perché:
• nel 75% dei casi, la pena sarebbe minore o uguale di quella ottenuta giocando da egoisti;
• nel 50% dei casi, la pena sarebbe addirittura minore di quella ottenuta giocando da egoisti;
• solo nel 25% dei casi, la pena sarebbe maggiore di quella ottenuta giocando da egoisti.
5.2 Implementazione
L’algoritmo qui implementato consiste nella fusione di due strategie precedentemente descritte: da una parte il lancio della moneta, dall’altra un particolare tipo di tit-for-tat che, invece di cambiare il comportamento, modifica di ±1 un valore in memoria (che rappresenta l’esito delle precedenti negoziazioni).
La strategia implementata, in sintesi, è la seguente:
Di volta in volta, la probabilità che un origin server modifichi la sua curva (che l’acquirente incrementi la sua proposta o che il venditore decrementi il suo prezzo) è del 500‰ (lancio della moneta), a cui va sommato il valore relativo all’esito delle precedenti negoziazioni con l’altro origin server: quando uno dei due origin server coinvolti modifica la sua curva, l’altro incrementa di uno il valore relativo all’esito delle precedenti negoziazioni con quell’origin server, viceversa, se non la modifica, l’altro decrementa di uno il suddetto valore (tit-for-tat).
La negoziazione va a buon fine se la proposta d’acquisto è maggiore o uguale al prezzo di vendita, entro dieci tentativi.
Successivamente, verranno descritte le contromisure previste in caso di fallimento delle negoziazioni.
5.3 Diagramma di flusso
⚠️
5.4 Esempi
⚠️
6. Simulatore CDG
⚠️
7. Valutazioni
Le simulazioni sono state effettuate generando, in modo random, di volta in volta, cinque CDG con le seguenti configurazioni:
1) 3 origin server, 15 replica server e 30 client;
2) 6 origin server, 30 replica server e 60 client;
3) 12 origin server, 60 replica server e 120 client;
4) 24 origin server, 120 replica server e 240 client;
5) 48 origin server, 240 replica server e 480 client.
Tutti i test riportati in questo capitolo sono stati effettuati su un computer Apple MacBook 2.1 (Mid 2007) con processore dual-core Intel Core 2 Duo a 2.0 GHz (con 4 MB di cache L2), 2 GB di memoria PC2-5300 a 667 MHz, scheda grafica Intel GMA 950 (con 64 MB di memoria), e sistema operativo Mac OS X Leopard (versione 10.5.1).
7.1 Configurazione 1
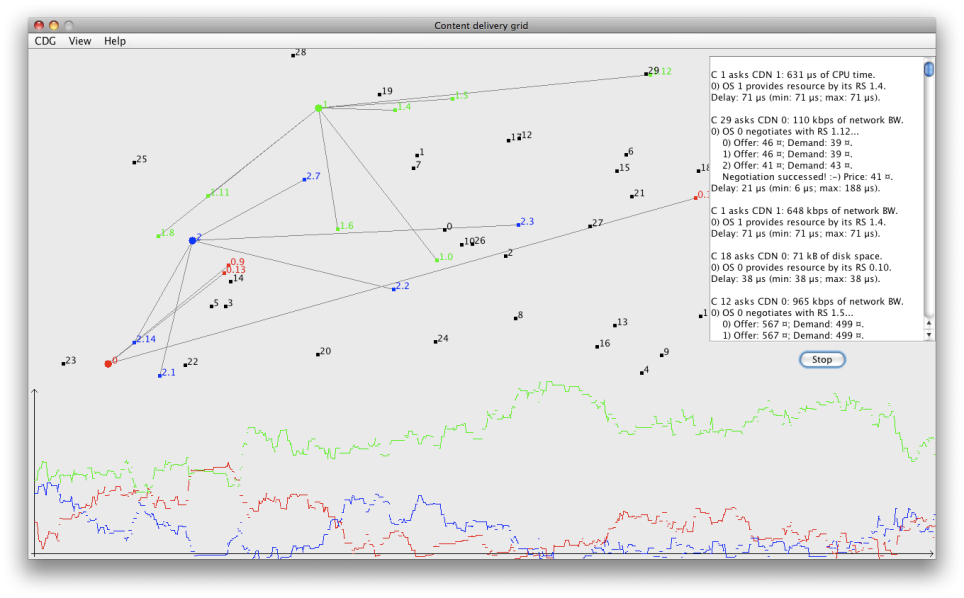
Figura 7.1: Andamento temporale dei crediti delle CDN appartenenti ad una CDG generata con configurazione 1.
| d [ms] | r | d / r [µs] | ||||
|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | |
| 174 | 135 | 218 | 1427 | 122 | 95 | 153 |
| 179 | 122 | 250 | 1378 | 129 | 88 | 181 |
| 199 | 134 | 226 | 1575 | 126 | 85 | 143 |
| 228 | 134 | 257 | 1437 | 159 | 93 | 179 |
| 246 | 179 | 325 | 1894 | 130 | 94 | 171 |
Tabella 7.1: Dati statistici (ritardo d e numero di richieste r) forniti da cinque CDG generate con configurazione 1.
7.2 Configurazione 2
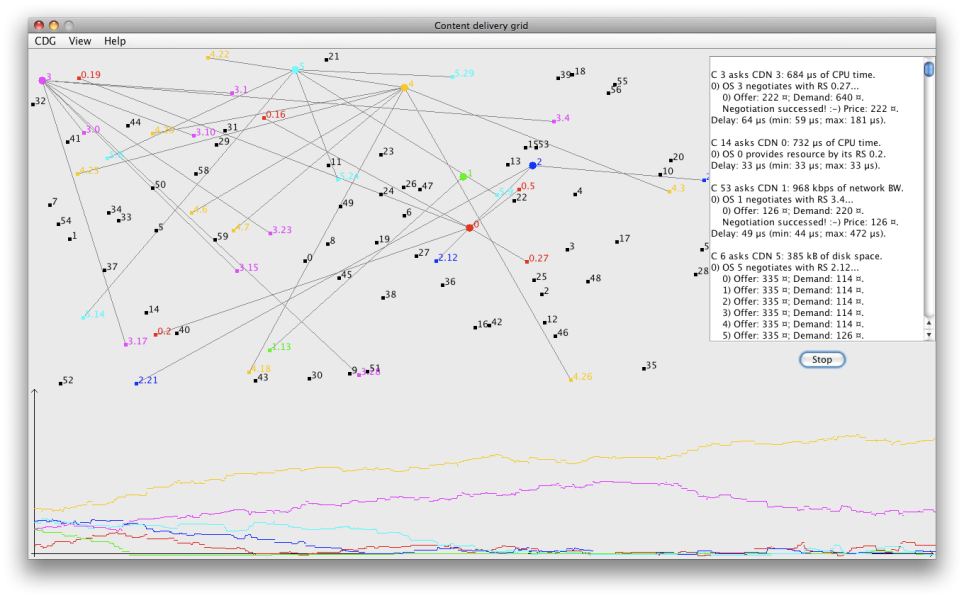
Figura 7.2: Andamento temporale dei crediti delle CDN appartenenti ad una CDG generata con configurazione 2.
| d [ms] | r | d / r [µs] | ||||
|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | |
| 200 | 107 | 261 | 1426 | 140 | 75 | 183 |
| 320 | 125 | 412 | 1851 | 173 | 68 | 222 |
| 165 | 88 | 245 | 1358 | 121 | 64 | 180 |
| 221 | 105 | 322 | 1801 | 123 | 58 | 179 |
| 141 | 75 | 235 | 1257 | 112 | 60 | 187 |
Tabella 7.2: Dati statistici (ritardo d e numero di richieste r) forniti da cinque CDG generate con configurazione 2.
7.3 Configurazione 3
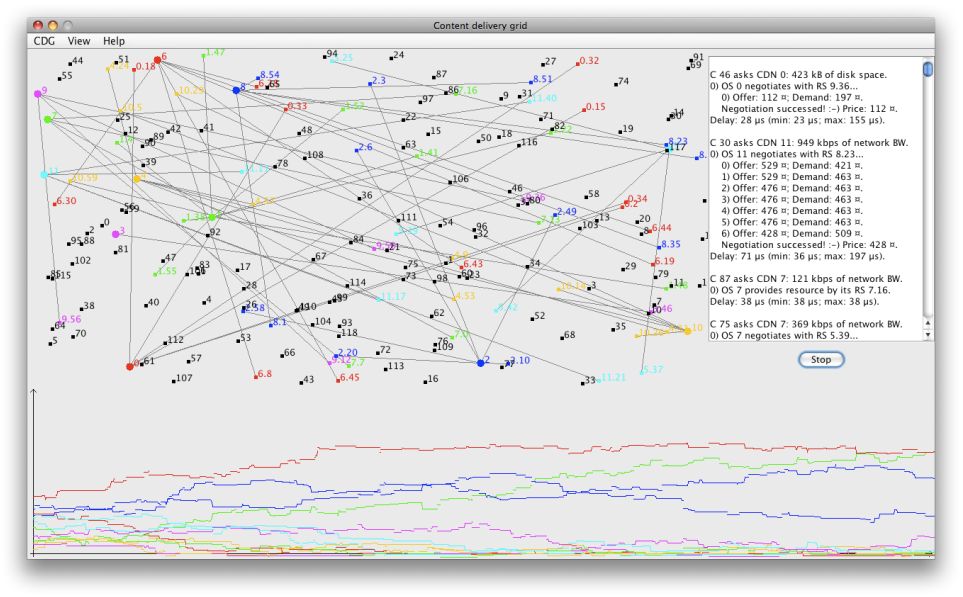
Figura 7.3: Andamento temporale dei crediti delle CDN appartenenti ad una CDG generata con configurazione 3.
| d [ms] | r | d / r [µs] | ||||
|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | |
| 274 | 100 | 436 | 2226 | 123 | 45 | 196 |
| 143 | 59 | 222 | 1384 | 103 | 43 | 161 |
| 256 | 95 | 393 | 2098 | 122 | 45 | 187 |
| 139 | 62 | 247 | 1229 | 113 | 51 | 201 |
| 154 | 65 | 273 | 1423 | 108 | 45 | 192 |
Tabella 7.3: Dati statistici (ritardo d e numero di richieste r) forniti da cinque CDG generate con configurazione 3.
7.4 Configurazione 4
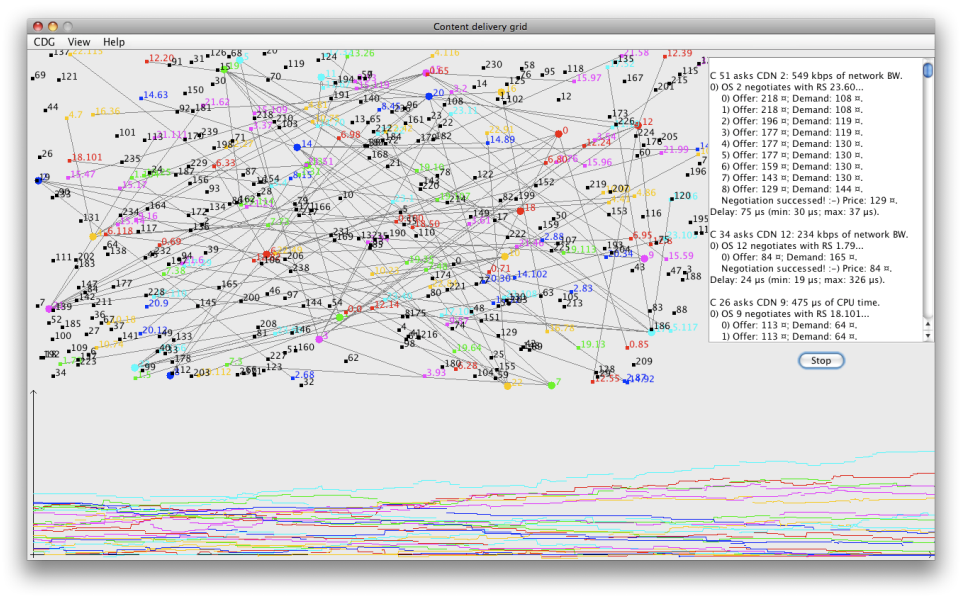
Figura 7.4: Andamento temporale dei crediti delle CDN appartenenti ad una CDG generata con configurazione 4.
| d [ms] | r | d / r [µs] | ||||
|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | |
| 158 | 63 | 235 | 1375 | 115 | 46 | 171 |
| 184 | 64 | 350 | 1969 | 93 | 32 | 178 |
| 117 | 38 | 254 | 1301 | 90 | 29 | 195 |
| 86 | 33 | 195 | 1087 | 79 | 31 | 180 |
| 181 | 52 | 328 | 1557 | 116 | 33 | 211 |
Tabella 7.4: Dati statistici (ritardo d e numero di richieste r) forniti da cinque CDG generate con configurazione 4.
7.5 Configurazione 5
Figura 7.5: Andamento temporale dei crediti delle CDN appartenenti ad una CDG generata con configurazione 5.
| d [ms] | r | d / r [µs] | ||||
|---|---|---|---|---|---|---|
| avg | min | max | avg | min | max | |
| 89 | 25 | 229 | 1173 | 76 | 22 | 195 |
| 117 | 31 | 286 | 1446 | 81 | 21 | 197 |
| 148 | 38 | 339 | 1780 | 83 | 21 | 190 |
| 95 | 26 | 230 | 1272 | 75 | 20 | 180 |
| 116 | 31 | 304 | 1507 | 77 | 20 | 201 |
Tabella 7.5: Dati statistici (ritardo d e numero di richieste r) forniti da cinque CDG generate con configurazione 5.
8. Conclusioni
Dai risultati ottenuti si evince che l’applicazione di questo modello è realmente vantaggiosa per lo scambio di documenti multimediali, poiché il tempo necessario per trasferire una risorsa (ritardo per richiesta) è complessivamente minore (del 10 ÷ 60%, a seconda della configurazione utilizzata) di quello impiegato da un protocollo che preveda soltanto la richiesta diretta ai replica server della propria organizzazione (ritardo per richiesta max).
L’installazione di questo sistema su un protocollo TCP/IP potrebbe recare grandi vantaggi ai fornitori di servizi di streaming video (tempi di attesa più brevi e, di conseguenza, un migliore sfruttamento della banda a disposizione), sotto l’ipotesi che si abbiano infrastrutture interne in grado di consentire la ridirezione dei flussi in modo continuo ed efficiente (ad esempio: una rete a fibre ottiche per la comunicazione fra i server).
(1) Il gioco d’azzardo è stato analizzato in tutte le sue forme ne Il giocatore (1866) di Fëdor Dostoevskij, che pubblicò questo libro soprattutto per pagarsi i debiti di gioco accumulati…
(2) Naturalmente questo vale da un punto di vista astratto, poiché presuppone che tutti gli individui abbiano sempre lo stesso concetto di razionalità. Non sorprendentemente, le strategie razionali si potranno quindi riformulare come variazioni di massime etiche ubique nella storia: la regola aurea di Confucio (dall’Analecta: «non fare agli altri ciò che non vorresti fosse fatto a te»), il precetto evangelico di Gesù (dal Vangelo secondo Matteo: «fai agli altri ciò che vorresti fosse fatto a te»), la regola di Hobbes (dal Leviatano: «quod tibi fieri non vis, alteri non feceris») e l’imperativo categorico di Kant (dalla Critica della ragion pratica: «fai ciò che vorresti che tutti facessero»).
(3) Sebbene questo dilemma sia stato sviluppato da Merrill Flood e Melvin Dresher, e formalizzato (e battezzato prisoner’s dilemma) da Albert Tucker (1950), in realtà risale almeno al Leviatano (1651) di Thomas Hobbes. L’idea di quest’ultimo era che le società umane siano alleanze rese necessarie del contenimento del violento stato di natura, fondato sull’aggressione contro tutti (non-cooperazione) e sulla paura di chiunque (cooperazione): una situazione, appunto, da dilemma del prigioniero. Mediante il contratto sociale, gli individui rinunciano al diritto di far violenza in cambio della sicurezza di essere protetti: il risultato è un cambiamento delle regole del gioco.
(4) Tit-for-tat (pan per focaccia) è un breve programma (soltanto quattro righe di codice!), scritto in Basic da Anatol Rapaport.
